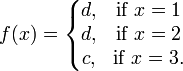โดเมน, โคโดเมน และเรนจ์
X ซึ่งคือเซตข้อมูลนำเข้าเรียกว่า โดเมนของ f และ Y ซึ่งคือเซตของผลลัพธ์ที่เป็นไปได้ เรียกว่า โคโดเมน เรนจ์ของ f คือเซตของผลลัพธ์จริงๆ {f (x) : x ในโดเมน} ระวังว่าบางครั้งโคโดเมนจะถูกเรียกว่าเรนจ์ เนื่องจากความผิดพลาดจากการจำแนกระหว่างผลที่เป็นไปได้กับผลจริงๆ
ฟังก์ชันนั้นเรียกชื่อตามเรนจ์ของมัน เช่น ฟังก์ชันจำนวนจริง หรือ ฟังก์ชันจำนวนเชิงซ้อน
เอนโดฟังก์ชัน คือฟังก์ชันที่โดเมนและเรนจ์เป็นเซตเดียวกัน
ในสาขาวิทยาการคอมพิวเตอร์ แบบชนิดข้อมูลของอาร์กิวเมนต์และค่าที่คืนกลับมาระบุโดเมนและโคโดเมน (ตามลำดับ) ของโปรแกรมย่อย ดังนั้นโดเมนและโคโดเมนจะถูกกำหนดไว้ในแต่ละฟังก์ชัน แต่เรนจ์จะเกี่ยวกับว่าค่าที่คืนกลับมาจะเป็นอย่างไร

 จากข้อมูลนำเข้าในเซต
จากข้อมูลนำเข้าในเซต  ไปยังผลที่เป็นไปได้ในเซต
ไปยังผลที่เป็นไปได้ในเซต  (เขียนเป็น
(เขียนเป็น  ) คือ
) คือ ใน
ใน  ใน
ใน 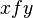 (
(  ผลลัพธ์เสมอ
ผลลัพธ์เสมอ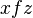 แล้ว
แล้ว 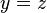 นั่นคือ ค่านำเข้าหลายค่าสามารถมีผลลัพธ์ได้ค่าเดียว แต่ค่านำเข้าค่าเดียวไม่สามารถมีผลลัพธ์หลายผลลัพธ์ได้
นั่นคือ ค่านำเข้าหลายค่าสามารถมีผลลัพธ์ได้ค่าเดียว แต่ค่านำเข้าค่าเดียวไม่สามารถมีผลลัพธ์หลายผลลัพธ์ได้
 โดยที่แต่ละค่าของ
โดยที่แต่ละค่าของ  อยู่ใน
อยู่ใน 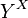 เรียกว่า
เรียกว่า (อ้างถึง
(อ้างถึง 
 ใน
ใน  และ
และ  ใน
ใน 

 หรือเป็น
หรือเป็น